Не обичаме да ви разочароваме, но за съжаление работата се оказа малко по-повече от очакваното, така че очакваната тестова мрежа е все още на няколко дни разстояние. Ще ви уведомим веднага щом бъде готова – това наистина може да бъде и след ден, но няма да изкушаваме съдбата, като прогнозираме.
Миналата седмица Дейвид Русу представи демонстрация на поверителни транзакции с пръстен (Ring CT) пред екипа. Беше увлекателно, но изпълнено с математиката, така че тази седмица ви представяме съкратена версия с минимум алгебра в опит да дадем малко предистория и да обясним посоката, в която вървим с частните DBC транзакции.
Общ напредък
Дейвид Русу, @danda и @Anselme се насочиха в различните аспекти на прилагането на пръстенови подписи, включително доказателства за плащане.
@ChrisO се бори мъжествено с GitHub Actions, за да се опита да направи тестовата мрежа достойна за пускане, но през последните няколко дни тя му се опъва.
@bochaco работи заедно с @chrisO, като се стреми да се справи с оставащите неуспешни CLI тестове и продължаваме да смачкваме все повече крайни случаи около разделянето на секциите.
Целият екип разглежда членството DKG – кой е най-ефективният начин да се гарантира, че Старейшините могат да следят Възрастните в техните секции и как можем да се предпазим от атаки за продажба на ключове, при които недоброжелател успешно купува контрол над секция?
Пръстенови подписи и Сейф
Искаме да похарчим DBC. За да направим това, трябва да докажем, че сме собственик. Но за да увеличим поверителността на нашите DBC транзакции, не искаме монетният двор да знае точно кои сме – което би станало, ако използваме стандартен ключ. Освен това монетният двор също трябва да знае, че този DBC вече не е изразходван.
За да постигнем тези цели, смятаме да използваме пръстенови подписи, надграждайки работата на Ring CT, извършена от Monero, и добавяйки Safe специфични неща като множествен подпис и доказателство за плащане.
Какво е пръстенов подпис?
Пръстеновите подписи са вероятностен метод за сигурност, а не криптографски затвърден такъв, но както Monero демонстрира, той също е много ефективен за анонимизиране на транзакции.
Пръстеновия подпис е начин за скриване на публичен ключ (в случая нашия ключ на собственик на DBC) сред много други ключове служещи за примамка. Пръстенът е само дума за група, така че в Safe нашият ключ е в пръстен с куп примамки, избрани на случаен принцип от група ключове, за които монетният двор знае.
Подписът, направен от който и да е ключ в пръстена, е валиден, но монетният двор не може да каже кой ключ в пръстена всъщност е подписал транзакция, а само че един от тях го е направил. Колкото по-голям е наборът от ключове за примамка, толкова по-трудно ще бъде за наблюдател на системата да отгатне действителния ключ, който е подписал транзакция.
Използваме пръстенов подпис, за да подпишем съобщение, като например заявка към монетен двор за преиздаване на DBC, за да можем да го похарчим. От този подпис монетният двор може да разбере, че съобщението е валидно, но не и кои сме ние. Може също така да провери дали нашият ключ не е бил използван преди, за да предотврати двойно харчене.
Самият пръстенов подпис съдържа (наред с други неща) ослепителна стойност (произволно число) за всяка от примамките и една за нашия ключ, плюс „образ на ключа“ за нашия ключ. Образа на ключа е репрезентиране на нашия ключ, което крие истинската му идентичност.
Няколко неща за отбелязване:
-
Всички ключове за примамка са били виждани от монетния двор преди. Те могат да бъдат ключове за собственост на други неизразходвани DBC или някои други валидни публични ключове.
-
Всеки пръстенов подпис може да се използва само веднъж.
-
Образа на ключа се съхранява в разходната книга, така че монетният двор може да каже, че вече е изразходван.
-
Създаването на нашия ключов образ изисква нашия таен ключ.
И така, какъв е нашият таен ключ? За да обясним това, трябва да отидем в криптографията с елиптична крива (ECC).
Криптография с елиптична крива
ECC е вид асиметрична криптография, която се използва от много криптовалути, включително биткойн. Както всички асиметрични криптосистеми, тя зависи от това, че изчисленията са лесни в едната посока и много трудни в другата, т.е. еднопосочни функции.
В ECC изчислението е как да стигнете от една точка на крива до друга. Ето как работи:
Да кажем, че имаме крива от вида: y2= x3 + ax + b.
Използваме кривата BLS12-381 (по-специално blstrs), която има такава форма:
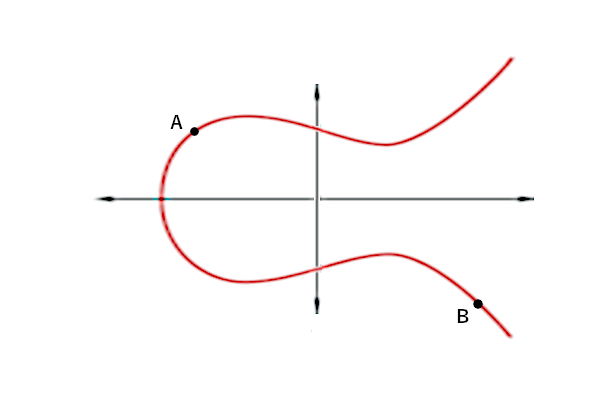
Кривата е огромна, покривайки крайно поле Fq, където q е много голямо просто число, което означава, че има огромен (но краен) брой възможни точки на кривата. Всички аритметични операции върху точки от кривата са по модул q. В модулната аритметика, след като стойността е по-голяма от q, тя се връща към началото отново, както при часовник: 3 + 10 modulo 12 = 1.
Когато умножим една точка от кривата ( A) с друга точка от кривата s, ще стигнем, привидно на случаен принцип, в друга точка (B), която също е на кривата. Правенето на това умножение е много бързо и лесно, но обръщането му - изработването на това, с което сме умножили точка “А”, за да стигнем до точка “Б” - обикновено ще отнеме хиляди години, тъй като по принцип трябва да прегледате всяка възможна опция докато не ударите правилната. Няма очевиден модел за това къде се появяват последователни точки на кривата и няма лесен начин процеса да бъде обърнат.
Има някои специални точки на тази крива, наречени генератори. Генераторът ( G) има свойството, че ако продължите да го добавяте към себе си (G, G+G, G+G+G ..) в крайна сметка той ще дефинира всяка възможна точка от кривата. Създаваме двойка ключове, като избираме G и го умножаваме по s, друга точка от кривата, известна само на нас.
sGе нашият публичен ключ,sе нашият таен ключ.
Добре, така че имаме нашия публичен ключ sG (който в нашия пример е ключa на собственик на DBC) и нашия таен ключ. Сега трябва да направим ключово изображение I. Формулата за това е:
I = sHp(sG)
Нашият ключов образ е тайния ни ключ s, умножен по хеша на публичния ни ключ sG. Нашият ключов образ „I“ е друга точка от кривата.
Имайте предвид, че тъй като нашият таен ключ s е необходим за създаване на I, само ние можем да го създадем. „I“ се съхранява в разходната книга.
Така че сега можем да докажем, че нашата идентичност е валидна с „I“, въпреки че нашият публичен ключ е хеширан и умножен по нашия таен ключ, а нашият публичен ключ е прикрит и смесен с всички други прикрити ключове за примамка. Монетният двор знае само, че един от тези ключове е правилният и ако нашия ключов образ се използва отново, той ще бъде намерен в разходната книга и блокиран.
Следващи стъпки
Дейвид Русу интегрира Ring CT в DBC кода. Следващата стъпка ще бъде да го накара да работи с BLS и след това да разгледа доказателството за плащане. @danda и @Anselme положиха основите тук. Идеята е да има фактури, които имат публични ключове за плащане и Педерсен ангажименти в тях. DBC за плащане ще бъде преиздадено, за да има точно същия ангажимент на Педерсен като този във фактурата. По този начин можем да докажем, че сме издали правилната сума и на правилния получател. Можем да публикуваме както фактурата, така и DBC за плащането публично, за да го видят всички, като предоставим доказателство, че сме платили тази фактура. Това е текущата ни работа.
Преводи:
![]() English
English ![]() Russian ;
Russian ; ![]() German ;
German ; ![]() Spanish ;
Spanish ; ![]() French
French
- Официален сайт на Safe Network
- Обобщено представяне на Safe Network
- Safe Network Фундаменти
- Карта на проекта
- Подробна информация може да намерите както винаги във форума на международната общност: Safe Network Forum
- Ако имате въпроси може да ги зададете във Facebook групата на българската Safe общност: Redirecting...
- Ако искате да следите последните новини заповядайте във Facebook страницата на Safe Network България: Safe Network България
